通原笔记 - 马特维尔兔窟

第三章信道与噪声part1

信道传输函数是常数(或者慢变化)的...叫恒参信道,传输函数随时间随机快变化,就叫随参信道.

调制信道的3种常用表示:

1.信道传输函数是常数,再加点高斯噪声...就是加性高斯噪声信道

2.信道传输函数在频带内不是常数,但不随时间变化...那就叫带加性噪声的线性滤波器信道 -.-好长

3.传输函数不是常数,还他妈随时间变来变去(我蒟蒻,想象无力)..书上说电离层反射信道\移动通信信道就这种...叫做:带有加性噪声的线性时变滤波器信道 -.-一个比一个长

编码信道跟上面的有点不一样..是离散的

这个貌似可以看成是集合映射神马的,然后由于万恶的噪声,每个元素有一定概率"射"到别的地方去-.-b,如果这个转移概率是没记忆的,~~那貌似就是一马尔可夫过程~~,如果有记忆...那就布吉岛了~

理想恒参信道的传输函数是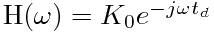 $H(\omega)=K_0e^{-j\omega t_d}$ ,就是这个信道除了对信号幅度上有点衰减,时间上有点延迟,就没什么别的了.

书提到的群延迟-频率特性貌似是相频特性的导数...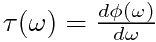 $\tau(\omega)=\frac{d\phi(\omega)}{d\omega}$ , 可是用来干啥,不懂

好吧..表述可能不准确...

信息量

*信息量是概率的函数:概率越小,信息量越大..

$I=log_a\frac{1}{P(x)}=-log_aP(x)$

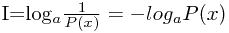
当底数取2是,信息量的单位是bit,是目前最常用的.

信息学的熵,大概是指符号的平均信息量:

$H(x)=\sum^n_{i=1}P(x_i)I(x_i)=-\sum^n_{i=1}P(x_i)log_aP(x_i)$

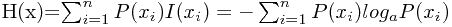
当每个符号出现的概率相等时,熵就最大了....

碼元

和比特不同一个概念..一个M进制碼元可以用一个 lb M 个二进制碼元表示..

碼元传输速率R_Bd 单位是波特(Baud)

信息传输速率R_b 就是经常听的比特率,单位是比特/秒(bit/s,b/s,bps)

上面两个东西的关系(貌似显然-.-0): 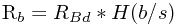$R_b=R_{Bd}*H (b/s)$ 那个H就是熵啦~

频带利用率η 书上有两种定义,一种是碼元传输速率比上带宽 , 另一种就系将碼元传输速率换成比特率

碼元差错率,信息差错率....脚趾头想想就知道的不写了,呃"信息差错率"的信息指比特...