马特维尔兔窟

这个牛B的筛法是在这里看到的

复杂度是线性的，扩展性超好～

自己YY了几个可以扩展的内容，权当模板～

#define N 1024
//niubee linear sevie method
int phi[N],//欧拉函数
    p[N],//素数表
    ld[N],//最小素因子
    ldt[N],//最小素因子的次数
    min_pk[N],//if p==ld[n],min_pk[n]=1+p+p^2+...+p^ldt[n];
    sig[N],//约数和
    nd[N];//因子数
//依赖性:min_pk<-sig;ldt<-nd;
void sevie()
{
	memset(p,0,sizeof(p));
	int i,j;

	phi[0]=0;phi[1]=1;//phi
	ld[0]=0;ld[1]=1;//ld
	ldt[0]=0;ldt[1]=1;//ldt
	min_pk[0]=0;min_pk[1]=1;//min_pk
	sig[0]=0;sig[1]=1;//sig
	nd[0]=0;nd[1]=1;//nd
	for(i=2;i<=N;i++)
	{
		if(!p[i]){
			p[++p[0]]=i;
			phi[i]=i-1;
			ld[i]=i;
			ldt[i]=1;
			min_pk[i]=i+1;
			sig[i]=i+1;
			nd[i]=2;
		}
		for(j=1;p[j]<=N/i;j++)
		{
			p[p[j]*i]=1;
			ld[p[j]*i]=p[j];
			if(i%p[j]){
				phi[p[j]*i]=phi[p[j]]*phi[i];
				ldt[p[j]*i]=1;
				min_pk[p[j]*i]=p[j]+1;
				sig[p[j]*i]=sig[i]*sig[p[j]];
				nd[p[j]*i]=nd[p[j]]*nd[i];
			}
			else{
				phi[p[j]*i]=phi[i]*p[j];
				ldt[p[j]*i]=ldt[i]+1;
				min_pk[p[j]*i]=p[j]*min_pk[i]+1;
				sig[p[j]*i]=sig[i]/min_pk[i]*min_pk[p[j]*i];
				nd[p[j]*i]=nd[i]/(ldt[i]+1)*(ldt[p[j]*i]+1);
				break;
			}
		}
	}
}

以前写容斥原理时,用的都是dfs~

今天突然想到...格雷碼,每次只改变一位,貌似可以用来写容斥原理;

然后就写了一个

const int BT[]={0,1,28,2,29,14,24,3,30,22,20,15,25,17,4,8,31,27,13,23,21,19,16,7,26,12,18,6,11,5,10,9};
#define BIT4CHG(i) BT[(unsigned int)((((i)+1)&~(i))*0x077CB531U)>>27]

其中的BIT4CHG,就是告诉你第i个格雷碼变成第i+1个时(i从0开始算),改变的是第几位~之所以可读性这么差是因为使用了这里的技巧.

这就避免了dfs递归了......

其实,这个效率确实提高不了多少~而且写起来没那么好看~

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define swap(a,b) do{a=a^b;b=a^b;a=a^b;}while(0)
typedef long long LL;
LL gcd(LL a,LL b)
{
	while(b){swap(a,b);b=b%a;}
	return a>0?a:-a;
}
LL mod_mult(LL a,LL b,LL mo)//ret:a*b%mo
{
	LL ret;
	a%=mo;
	for(ret=0;b;a=(a<<1)%mo,b>>=1)
		if(b&1)
			ret=(ret+a)%mo;
	return ret;
}
LL mod_exp(LL a,LL b,LL mo)//ret:a^b%mo
{
	LL ret=1,temp=a%mo;
	for(;b;b>>=1,temp=mod_mult(temp,temp,mo))
		if(b&1)
			ret=mod_mult(ret,temp,mo);
	return ret;
}
LL pollard_rho(LL n,int c)
{
	LL x,y,d,i=1,k=2;
	x=rand()%(n-1)+1;
	y=x;
	while(1)
	{
		i++;
		x=(mod_mult(x,x,n)+c)%n;
		d=gcd(y-x,n);
		if(d>1&&d<n)return d;
		if(x==y)return n;
		if(i==k)y=x,k<<=1;
		//if(k>1<<11)return n;
	}
}

int miller_rabin(LL n,int time)
{
	if (n==2||n==3||n==5||n==7)return 1;
	if (n<2||!(n&1))return 0;
	int i,j,t=0;
	LL a,x,y,u=n-1;
	while((u&1)==0) t++,u>>=1;
	for(i=0;i<time;i++)
	{
		a=rand()%(n-1)+1;
		x=mod_exp(a,u,n);
		for(j=0;j<t;j++)
		{
			y=mod_mult(x,x,n);
			if (y==1&&x!=1&&x!=n-1)
				return 0;
			x=y;
		}
		if (x!=1)
			return 0;
	}
	return 1;
}
LL min;
void fuck(LL i)
{
	LL x;
	if(miller_rabin(i,8)){if(i<min)min=i;/*printf(" %lld ",i);*/return;}
	do{x=pollard_rho(i,rand()%15+2);}while((x==1||x==i));
	fuck(x);
	fuck(i/x);
}
int main()
{
	LL i;int t;
	scanf("%d",&t);
	while(t--){
	scanf("%lld",&i);
	min=i;
	fuck(i);
	if(i!=min)printf("%lld\n",min);
	else printf("Prime\n");}
	return 0;
}

曼哈顿距离是什么-->http://zh.wikipedia.org/zh-hant/%E6%9B%BC%E5%93%88%E9%A0%93%E8%B7%9D%E9%9B%A2

经过冗长的推导会发现这个等式成立

d=|x1-x2|+|y1-y2|

=max{(x1+x2)-(y1+y2) , (x1-x2)-(y1-y2) , (-x1+x2)-(-y1+y2) , (-x1-x2)-(-y1-y2)}

计算两点间的曼哈顿距离，这式子完全没用，但是，给定N个点，求他们的最大哈密顿点对是，就很好用了。

朴素方法算复杂度是O(N²)，而利用这个式子复杂度为O(N*2^k)，k是维度，上面写的是2维的情况，高维情况类比可得。

kruskal：
输入：边集E

for each <u,v> in E

        //用并查集实现

        if u.root != v.root //u v 不在同一集合（不会产生回路）

             union(u,v)//加入变<u,v>

合并同时记录边数，由于n个点的生成树只有n-1条边，一旦加够了，就停

//并查集的实现

int root[MAXN];//记录每个节点的根节点

void init(int x)//初始化
{
     for(int i=0;i<x;i++)root[i]=i;//每个节点开始时独立
}

int getroot(int x)//取出根节点，顺便压缩路径
{
    if(x!=root[x])root[x]=getroot(root[x]);
    return root[x];
}

inline int unionset(int x1,int x2)//合并俩集合
{
    int a=getroot(x1),b=getroot(x2);
    root[a]=b;
}

辗转相除法最大公约数:

//要求a,b不同时为零
int gcd(int a,int b)
{
    if(!b)return a;
    else return gcd(b,a%b);
}

利用最大公约数求最小公倍数:

int lcm(int a,int b)
{
    if(!(a*b))return 0;
    else return a*b/gcd(a,b);
} 

求: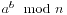

int modExp(int a,int b,int n)
{
    int t=1,y=(a%n+n)%n;
    while(b)
    {
            if(b%2==1)t=t*y%n;
            y=y*y%n;
            b/=2;
    }
    return t;
}

扩展的Euclid算法:

//返回a，b的最大公约数d，并使ax+by=d
int ExtEuclid(int a,int b,int *x,int *y)
{
    int d,tmp;
    if(b==0)
    {
            *x=1;
            *y=0;
            return a;
    }
    d=ExtEuclid(b,a%b,x,y);
    tmp=*x;
    *x=*y;
    *y=tmp-a/b*(*x);
    return d;
}

解线性同余方程: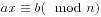

//返回最小的x...通解是X=x(mod n/d) 
int modularLinerEquation(int a,int b,int n)
{
    int x,y,d;
    d=ExtEuclid(a,n,&x,&y);
    if(b%d!=0)return -1; // no solution
    x=b/d*x;
    x=(x%(n/d)+(n/d))%(n/d);
    return x; 
}

用中国剩余定理解同余方程组: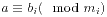

//用中国剩余定理解线性同与方程组$a\equiv b_i(\mod m_i)$
int solModularEquations(int b[],int m[],int z)
{
    int M=1,i,y,result=0;
    for(i=0;i<z;i++)M*=m[i];
    for(i=0;i<z;i++)
    {
        y=modularLinerEquation(M/m[i],1,m[i]);
        result=(result+y*b[i]*M/m[i])%M;
    }
    return result;
}

Miller-Rabin测试:

//Miller-Rabin素性测试
//令大奇数$n=2^lm+1$,其中l非负整数,m为正奇数.
//若$b^m\equiv 1(\mod n)$或者$b^{2^jm}\equiv -1(\mod n)$ ,0<=j<=l-1
//则称n通过以b为基的miller-rabin测试 
int passMillerRabinTest(int n) 
{
    int l,m;
    m=n-1;
    l=0;
    while(m%2==0)
    {
        l++;
        m/=2;
    }
    
    b=rand()%(n-1)+1;
    
    if(modExp(b,m,n)==1)return 1;
    
    int i,k;
    k=m;
    for(i=0;i<l;i++)
    {
        if(modExp(b,k,n)==n-1)return 1;
        k*=2;
    }
    
    return 0;
}