辗转相除法最大公约数:

//要求a,b不同时为零
int gcd(int a,int b)
{
    if(!b)return a;
    else return gcd(b,a%b);
}

利用最大公约数求最小公倍数:

int lcm(int a,int b)
{
    if(!(a*b))return 0;
    else return a*b/gcd(a,b);
} 

求: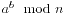

int modExp(int a,int b,int n)
{
    int t=1,y=(a%n+n)%n;
    while(b)
    {
            if(b%2==1)t=t*y%n;
            y=y*y%n;
            b/=2;
    }
    return t;
}

扩展的Euclid算法:

//返回a，b的最大公约数d，并使ax+by=d
int ExtEuclid(int a,int b,int *x,int *y)
{
    int d,tmp;
    if(b==0)
    {
            *x=1;
            *y=0;
            return a;
    }
    d=ExtEuclid(b,a%b,x,y);
    tmp=*x;
    *x=*y;
    *y=tmp-a/b*(*x);
    return d;
}

解线性同余方程: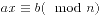

//返回最小的x...通解是X=x(mod n/d) 
int modularLinerEquation(int a,int b,int n)
{
    int x,y,d;
    d=ExtEuclid(a,n,&x,&y);
    if(b%d!=0)return -1; // no solution
    x=b/d*x;
    x=(x%(n/d)+(n/d))%(n/d);
    return x; 
}

用中国剩余定理解同余方程组: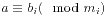

//用中国剩余定理解线性同与方程组$a\equiv b_i(\mod m_i)$
int solModularEquations(int b[],int m[],int z)
{
    int M=1,i,y,result=0;
    for(i=0;i<z;i++)M*=m[i];
    for(i=0;i<z;i++)
    {
        y=modularLinerEquation(M/m[i],1,m[i]);
        result=(result+y*b[i]*M/m[i])%M;
    }
    return result;
}

Miller-Rabin测试:

//Miller-Rabin素性测试
//令大奇数$n=2^lm+1$,其中l非负整数,m为正奇数.
//若$b^m\equiv 1(\mod n)$或者$b^{2^jm}\equiv -1(\mod n)$ ,0<=j<=l-1
//则称n通过以b为基的miller-rabin测试 
int passMillerRabinTest(int n) 
{
    int l,m;
    m=n-1;
    l=0;
    while(m%2==0)
    {
        l++;
        m/=2;
    }
    
    b=rand()%(n-1)+1;
    
    if(modExp(b,m,n)==1)return 1;
    
    int i,k;
    k=m;
    for(i=0;i<l;i++)
    {
        if(modExp(b,k,n)==n-1)return 1;
        k*=2;
    }
    
    return 0;
}