hud4048

MATWETU posted @ 2011年9月21日 13:01 in 未分类 with tags 数论容斥原理积性函数组合 , 1483 阅读

参考完核武报告,没完全懂~翻了翻组合数学书,这实质上就是求元素可重复的圆排列--许多组合数学书里讲莫比乌斯反演时唯一的例题~

先求 r 种不同元素,放在圆的n个点上 , 有几种放法, 旋转后相同算一种.

做法是:设周期为为d,d|n,的方案数是Td(r) 则每个这样的圆排列,对应着d个线排列

线排列总数是r^n,所以:

$r^n = \sum_{d|n} d\cdot T_d(r)$

莫比乌斯反演后:

$n\cdot T_n(r) = \sum_{d|n}\mu(n/d)\cdot r^{d}$

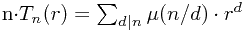
总的方案数M_n就是各种周期的和:

$M_n(r) = \sum_{k|n}\frac{1}{k}\sum_{d|k}\mu(k/d)\cdot r^{d}$

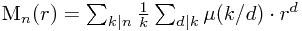
因 d|k|n , 设k'=k/d . n'=n/d

$M_n(r) = \sum_{\frac{k}{d}|\frac{n}{d}}\sum_{d|n}\frac{1}{k}\mu(k/d)\cdot r^{d}$

$M_n(r) = \sum_{d|n}\frac{r^d}{n}\sum_{{k^,}|{n^,}}\mu(k^,)\cdot \frac{n^,}{k^,}$

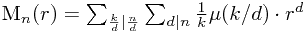
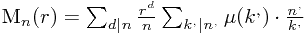
注意到后面一部分和等于n'的欧拉函数,故Mn可以写成:

$M_n(r) = \frac{1}{n}\sum_{d|n}\phi(n/d)\cdot r^d$

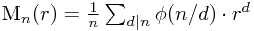
问题基本解决,剩下就是核武报告里说差不多,把最小公约数是i的倍数的方法数求出,容斥原理搞搞.

最后的答案应该是:

$ANS=\sum_{n=1}^{maxWeight} \mu(n)\cdot \frac{1}{n}\sum_{d|n}\phi(n/d)\cdot r_n^d$

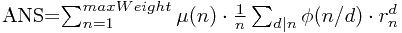
其中r_n表示重量是n的倍数的石子种数

mu(n) 和 phi(n) 都可以在预处理时筛出来,

n的分解只需要搞一遍就够了~

遗憾的是,还是很慢,board的第一名时空复杂度都比我写的好~ym

马特维尔兔窟