codeforce 17D Notepad
这题实际求的是\(a^b\ mod\ n\),但是\(gcd(a,n)\)[下面记作(a,n)]不一定等于1.......
(a,n)等于1时直接费马小定理能推倒...
(a,n)不为1时,有如下事实(当然互素时显然成立):
\[a^{2\phi (n)}\ mod\ n = a^{\phi (n)}\ mod\ n\]
即
\[a^{\phi (n)}(a^{\phi(n)}-1)\ mod \ n =0\]
简单证明如下:
1.如果\(a^{\phi (n)}\ mod \ n =0\),等式显然成立.
2.否则,命题等价于
\[\frac{a^{\phi (n)} }{(a^{\phi (n)},n)} (a^{\phi (n)}-1) \ mod \ \frac{n}{(a^{\phi (n)} ,n)} = 0\]
即:
\[a^{\phi (n)}\ mod \ \frac{n}{(a^{\phi (n)} ,n)} = 1\]
到这里就能使用费马小定理了~
回到题目上:\(a^b\ mod\ n\)$实际上分两种情况:
1.\(b<\phi (n)\),此时直接算
2.else,\(a^b\ mod\ n=a^{b\ mod\ \phi (n)+\phi (n)}\ mod\ n\)
对任意(?)a,n成立
SPOJ3871 GCDEX
这题的描述对我这种语言能力残缺的人来说,复述起来太难:
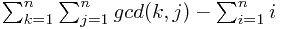
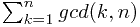,然后累加一下...额累加时第i项还要减个i~
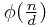个~这意味着:
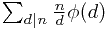;现在证明,T(n)是一个积性函数
证明:
设 m , n 满足 (m,n)=1:
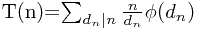
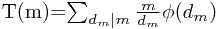
则:
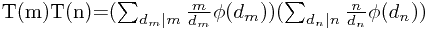
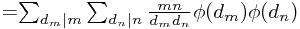
由于(m,n)=1,故dn与dm互素,所有dn,dm的组合正好取遍mn的约数
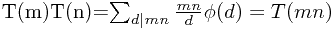
到了这里,只需考虑n等于素数的幂时T(n)的值:
根据T(n)的定义,显然有:
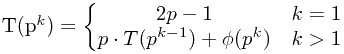
有了这个性质,就有可以在O(n)时间内用这个 牛X的筛法 把表打出来,然后求和还是O(n),查询什么的显然O(1)咯lol...
代码:
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#define FF(i,b) for(i=0;i<(b);i++)
#define FOR(i,a,b) for(i=(a);i<=(b);i++)
#define ZERO(x) do{memset(x,0,sizeof(x));}while(0)
#define SWAP(a,b) do{int _tmp=a;a=b;b=_tmp;}while(0)
#define INFI 2000000000
#define INFF 1e100
#define maxn 1000000
typedef long long LL;
int p[maxn+1],ph[maxn+1],pk[maxn+1],T[maxn+1];
LL G[maxn+1];
void sevie()
{
memset(p,0,sizeof(p));
int i,j;
p[0]=ph[0]=0;ph[1]=1;T[1]=1;
for(i=2;i<=maxn;i++)
{
if(!p[i]){p[++p[0]]=i;ph[i]=i-1;pk[i]=i;T[i]=(i<<1)-1;}
for(j=1;p[j]<=maxn/i;j++)
{
p[p[j]*i]=1;
if(i%p[j]){
ph[i*p[j]]=ph[i]*p[j];
pk[i*p[j]]=p[j];
T[i*p[j]]=T[i]*T[p[j]];
}
else{
ph[i*p[j]]=ph[i]*p[j];
pk[i*p[j]]=pk[i]*p[j];
if(i==pk[i])T[i*p[j]]=p[j]*T[i]+ph[i*p[j]];
else T[i*p[j]]=T[i/pk[i]]*T[pk[i]*p[j]];
break;
}
}
}
G[0]=0;
for(i=1;i<=maxn;i++)G[i]=G[i-1]+T[i]-i;
}
int main ( int argc, char *argv[] )
{
sevie();
int n;
while(scanf("%d",&n)!=EOF)
{
if(!n)break;
printf("%lld\n",G[n]);
}
return EXIT_SUCCESS;
}
牛逼的线性时间筛法
这个牛B的筛法是在这里看到的
复杂度是线性的，扩展性超好～
自己YY了几个可以扩展的内容，权当模板～
#define N 1024
//niubee linear sevie method
int phi[N],//欧拉函数
p[N],//素数表
ld[N],//最小素因子
ldt[N],//最小素因子的次数
min_pk[N],//if p==ld[n],min_pk[n]=1+p+p^2+...+p^ldt[n];
sig[N],//约数和
nd[N];//因子数
//依赖性:min_pk<-sig;ldt<-nd;
void sevie()
{
memset(p,0,sizeof(p));
int i,j;
phi[0]=0;phi[1]=1;//phi
ld[0]=0;ld[1]=1;//ld
ldt[0]=0;ldt[1]=1;//ldt
min_pk[0]=0;min_pk[1]=1;//min_pk
sig[0]=0;sig[1]=1;//sig
nd[0]=0;nd[1]=1;//nd
for(i=2;i<=N;i++)
{
if(!p[i]){
p[++p[0]]=i;
phi[i]=i-1;
ld[i]=i;
ldt[i]=1;
min_pk[i]=i+1;
sig[i]=i+1;
nd[i]=2;
}
for(j=1;p[j]<=N/i;j++)
{
p[p[j]*i]=1;
ld[p[j]*i]=p[j];
if(i%p[j]){
phi[p[j]*i]=phi[p[j]]*phi[i];
ldt[p[j]*i]=1;
min_pk[p[j]*i]=p[j]+1;
sig[p[j]*i]=sig[i]*sig[p[j]];
nd[p[j]*i]=nd[p[j]]*nd[i];
}
else{
phi[p[j]*i]=phi[i]*p[j];
ldt[p[j]*i]=ldt[i]+1;
min_pk[p[j]*i]=p[j]*min_pk[i]+1;
sig[p[j]*i]=sig[i]/min_pk[i]*min_pk[p[j]*i];
nd[p[j]*i]=nd[i]/(ldt[i]+1)*(ldt[p[j]*i]+1);
break;
}
}
}
}