马特维尔兔窟

codeforce 17D Notepad

这题实际求的是$a^b\ mod\ n$,但是$gcd(a,n)$[下面记作(a,n)]不一定等于1.......

(a,n)等于1时直接费马小定理能推倒...

(a,n)不为1时,有如下事实(当然互素时显然成立):

\[a^{2\phi (n)}\ mod\ n = a^{\phi (n)}\ mod\ n\]

即

\[a^{\phi (n)}(a^{\phi(n)}-1)\ mod \ n =0\]

简单证明如下:

1.如果$a^{\phi (n)}\ mod \ n =0$,等式显然成立.

2.否则,命题等价于

\[\frac{a^{\phi (n)} }{(a^{\phi (n)},n)} (a^{\phi (n)}-1) \ mod \ \frac{n}{(a^{\phi (n)} ,n)} = 0\]

即:

\[a^{\phi (n)}\ mod \ \frac{n}{(a^{\phi (n)} ,n)} = 1\]

到这里就能使用费马小定理了~

回到题目上:$a^b\ mod\ n$$实际上分两种情况:

1.$b<\phi (n)$,此时直接算

2.else,$a^b\ mod\ n=a^{b\ mod\ \phi (n)+\phi (n)}\ mod\ n$

对任意(?)a,n成立

第三章信道与噪声part1

信道传输函数是常数(或者慢变化)的...叫恒参信道,传输函数随时间随机快变化,就叫随参信道.

调制信道的3种常用表示:

1.信道传输函数是常数,再加点高斯噪声...就是加性高斯噪声信道

2.信道传输函数在频带内不是常数,但不随时间变化...那就叫带加性噪声的线性滤波器信道 -.-好长

3.传输函数不是常数,还他妈随时间变来变去(我蒟蒻,想象无力)..书上说电离层反射信道\移动通信信道就这种...叫做:带有加性噪声的线性时变滤波器信道 -.-一个比一个长

编码信道跟上面的有点不一样..是离散的

这个貌似可以看成是集合映射神马的,然后由于万恶的噪声,每个元素有一定概率"射"到别的地方去-.-b,如果这个转移概率是没记忆的,~~那貌似就是一马尔可夫过程~~,如果有记忆...那就布吉岛了~

理想恒参信道的传输函数是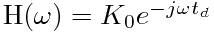 $H(\omega)=K_0e^{-j\omega t_d}$ ,就是这个信道除了对信号幅度上有点衰减,时间上有点延迟,就没什么别的了.

书提到的群延迟-频率特性貌似是相频特性的导数...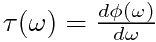 $\tau(\omega)=\frac{d\phi(\omega)}{d\omega}$ , 可是用来干啥,不懂

通原第一章-绪论

好吧..表述可能不准确...

信息量

*信息量是概率的函数:概率越小,信息量越大..

$I=log_a\frac{1}{P(x)}=-log_aP(x)$

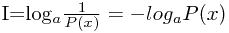
当底数取2是,信息量的单位是bit,是目前最常用的.

信息学的熵,大概是指符号的平均信息量:

$H(x)=\sum^n_{i=1}P(x_i)I(x_i)=-\sum^n_{i=1}P(x_i)log_aP(x_i)$

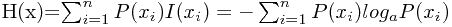
当每个符号出现的概率相等时,熵就最大了....

碼元

和比特不同一个概念..一个M进制碼元可以用一个 lb M 个二进制碼元表示..

碼元传输速率R_Bd 单位是波特(Baud)

信息传输速率R_b 就是经常听的比特率,单位是比特/秒(bit/s,b/s,bps)

上面两个东西的关系(貌似显然-.-0): 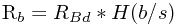$R_b=R_{Bd}*H (b/s)$ 那个H就是熵啦~

频带利用率η 书上有两种定义,一种是碼元传输速率比上带宽 , 另一种就系将碼元传输速率换成比特率

碼元差错率,信息差错率....脚趾头想想就知道的不写了,呃"信息差错率"的信息指比特...

矩阵乘法结果的检验---Freivalds' algorithm

逛Uva的时候,看到了一个题,模型很简单,让验证一个矩阵是不是另一个矩阵的平方...朴素O(n^3)果断超时;看题解,原来是个随机算法-.-,思想和米勒拉宾素性测试很像,http://en.wikipedia.org/wiki/Freivalds'_algorithm

算法基于这么个事实:设X是一个随机向量,xi在{0,1,2...t}中任意选取;那么对于不同的矩阵A,B ,AX=BX的概率最多只有1/(t+1)

不严谨的证一下...

如果A != B ,而AX == BX 那必然有 (A-B)X==0 , 且 H=A-B != 0 ...

最坏情况呢...就是H的没个行向量都一样...就记为 h 吧, 既然非零,总有个hi != 0的

h1*x1+h2*x2+...+hn*xn==0 ==> xi=(h1*x1+...h_i-1*x_i-1+h_i+1*x_i+1+...hn*xn)/(-hi)

xi是0~t随机选的,他刚好满足这个条件的概率就是1/(t+1)...

那矩阵来乘个列向量,撑死是O(n^2)...做上几次测试,几乎就是必然了...更不必说那个1/(t+1)是个上界...

codeforce 111D Petya and Coloring

公式都化出来的,居然还要对着数据调了半天....囧

题意大概是:给你一个n*m的棋盘和k种颜色,求满足要求的涂色方案,额...要求就是:垂直方向把棋盘分成两边(非空),不管怎么分,两边的颜色种数相等....

满足要求的方案首先要最左最右的满足颜色数相等,然后中间,在最左和最右边的交集中随意取;

最后化出来就是: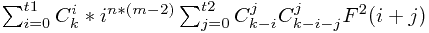 $\sum_{i=0}^{t1}C_k^i*i^{n*(m-2)}\sum_{j=0}^{t2}C_{k-i}^j C_{k-i-j}^j F^2(i+j)$

t1=min(m,k),t2=min(m-i,(k-i)/2);

这个F(x)表示x种颜色填到n个格子里,每种至少一个,有多少种涂法:

F(1)=1,F(x)=x^n-F(x-1)-F(x-2)-...-F(1);

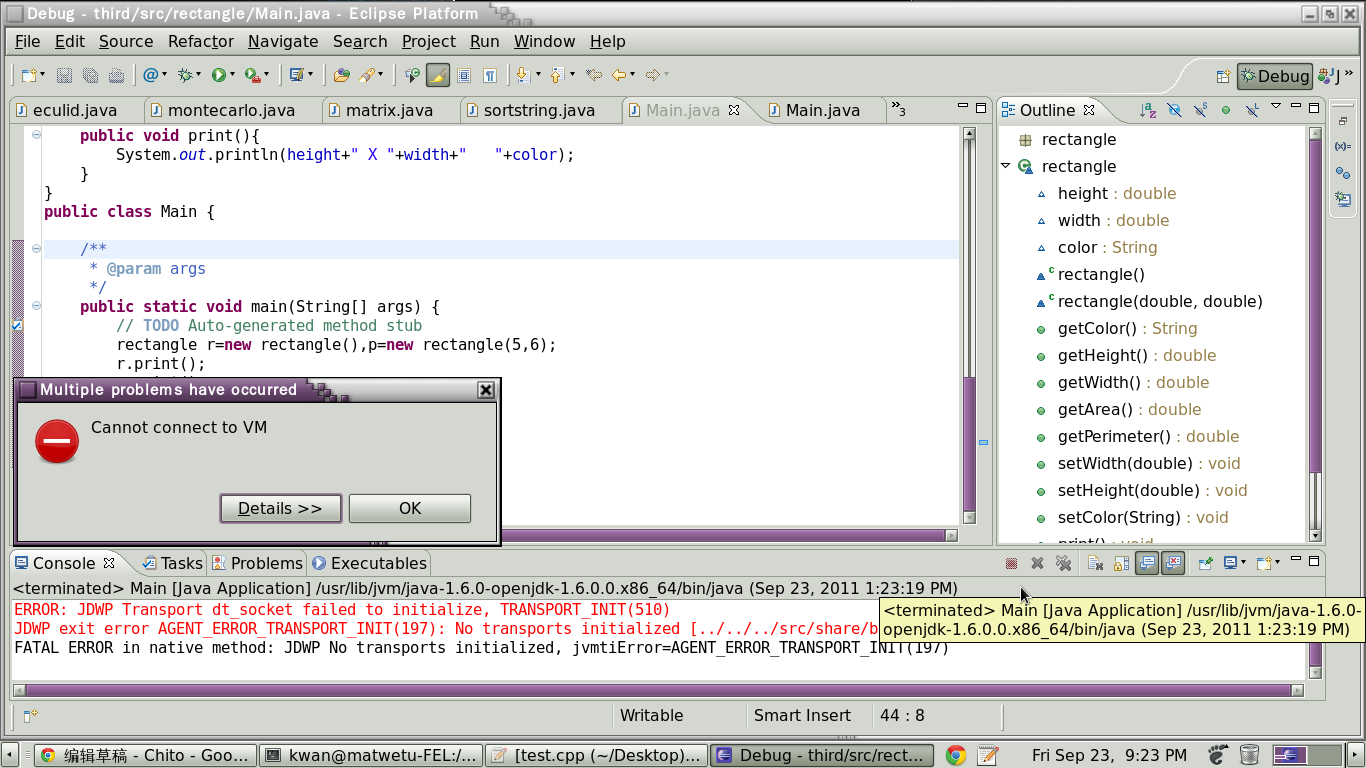
上网查,有人说是"From this (http://forum.java.sun.com/thread.jspa?threadID=618145) it seems that Eclipse is trying to connect to your external IP instead of localhost." 原文:http://forums.fedoraforum.org/archive/index.php/t-97415.html

于是在/etc/hosts里加了句127.0.0.1 localhost

问题解决了

hud4048

核武的思路:http://hi.baidu.com/aekdycoin/blog/item/69e075f5e200bcf47709d769.html

参考完核武报告,没完全懂~翻了翻组合数学书,这实质上就是求元素可重复的圆排列--许多组合数学书里讲莫比乌斯反演时唯一的例题~

先求 r 种不同元素,放在圆的n个点上 , 有几种放法, 旋转后相同算一种.

做法是:设周期为为d,d|n,的方案数是Td(r) 则每个这样的圆排列,对应着d个线排列

线排列总数是r^n,所以:

$r^n = \sum_{d|n} d\cdot T_d(r)$

莫比乌斯反演后:

$n\cdot T_n(r) = \sum_{d|n}\mu(n/d)\cdot r^{d}$

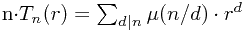
总的方案数M_n就是各种周期的和:

$M_n(r) = \sum_{k|n}\frac{1}{k}\sum_{d|k}\mu(k/d)\cdot r^{d}$

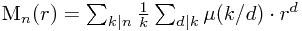
因 d|k|n , 设k'=k/d . n'=n/d

$M_n(r) = \sum_{\frac{k}{d}|\frac{n}{d}}\sum_{d|n}\frac{1}{k}\mu(k/d)\cdot r^{d}$

$M_n(r) = \sum_{d|n}\frac{r^d}{n}\sum_{{k^,}|{n^,}}\mu(k^,)\cdot \frac{n^,}{k^,}$

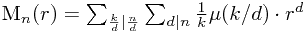
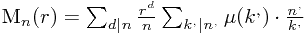
注意到后面一部分和等于n'的欧拉函数,故Mn可以写成:

$M_n(r) = \frac{1}{n}\sum_{d|n}\phi(n/d)\cdot r^d$

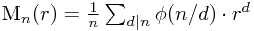
问题基本解决,剩下就是核武报告里说差不多,把最小公约数是i的倍数的方法数求出,容斥原理搞搞.

最后的答案应该是:

$ANS=\sum_{n=1}^{maxWeight} \mu(n)\cdot \frac{1}{n}\sum_{d|n}\phi(n/d)\cdot r_n^d$

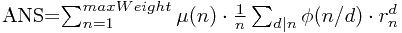
其中r_n表示重量是n的倍数的石子种数

mu(n) 和 phi(n) 都可以在预处理时筛出来,

n的分解只需要搞一遍就够了~

遗憾的是,还是很慢,board的第一名时空复杂度都比我写的好~ym

catalan number~卡塔兰数\卡特兰数...

http://en.wikipedia.org/wiki/Catalan_number

catalan数的身世,wiki(上面链接)有....那里还提供了5种(?)求法~第一种:母函数,第二种:全体数-非法数,第三种:通过定义一个叫exceedance的玩意,然后通过一个很奇葩的构造,说明exceedance等于0,1,2...n的路径数相等,直接得出结果~第四种是基于卡特兰数在多边形的三角划分的,推出个递推式~第五种是根据递推式,死推~

昨天,上海网赛热身,那题http://acm.hdu.edu.cn/showproblem.php?pid=4015, 是一个很像很像catalan数的玩意~大概是:给你两种数,a,b,权值分别是1和-m , a有k*m+1个,m有k个 , 问有几种排列方法,使得前任意项的和都不为0;

m取1时,就是红果果的catalan数~

m!=1时 ~ 不会..不过又找到了卡特兰数一个牛B的不同于wiki那5种的求法,完全兼容上面那题~这是本文存在的原因~

原文在这里,里面还有好几种别的求法:谷歌文档~偷来了,怕丟不好意思

现在说说那个求法:

给你n+1个'/'和n个'\' , 让你用这些随意的首尾相接组到一起, 一共就C(2n+1,n)种组法,我们要求的是除起点外所有点的海拔都大于0的组合数;

每种(含非法)组法就称为一个pattern , 显然这些pattern有一个性质,最后那点比第一点高出一个单位;

还有一个不那么显然的性质:在连接最后一点和第一点的直线上,没有一个\或/的端点落在上面,这是因为最后那点才是1,落在上面就意味着有分数,这不可能;

高潮来了~现在把两个相同的pattern首位相接,从前面不同的2n+1位开始的2n+1位,一共有2n+1个不同(why?我再想想)的pattern:其中,只有一个是合法的!!!(想象一条斜率为1/(2n+1)的直线从底部缓缓升起)

so~总的合法序列就C(2n+1,n)/(2n+1)个~

用这个来做上面的那道题,没压力啊,连化简都省了,直接出结果啊!~~~

SPOJ3871 GCDEX

这题的描述对我这种语言能力残缺的人来说,复述起来太难:

3871. GCD Extreme

Problem code: GCDEX

Given the value of N, you will have to find the value of G. The meaning of G is given in the following code

G=0;

for(k=i;k< N;k++)

for(j=i+1;j<=N;j++)

{

G+=gcd(k,j);

}

/*Here gcd() is a function that finds the greatest common divisor of the two input numbers*/

Input

The input file contains at most 20000 lines of inputs. Each line contains an integer N (1Output for each line of input produce one line of output. This line contains the value of G for the corresponding N. The value of G will fit in a 64-bit signed integer.

实质上是求这么一个东西: G(n)= $\sum_{k=1}^{n}\sum_{j=1}^{n}gcd(k,j)-\sum_{i=1}^{n}i$

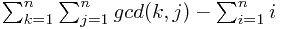
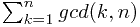求G(n)的话,可以先求T(n)= $\sum_{k=1}^{n}gcd(k,n)$ ,然后累加一下...额累加时第i项还要减个i~

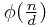如果学过数论,应该有印象,小于n的数里gcd(i,n)=d的i一共有 $\phi(\frac{n}{d})$ 个~这意味着:

T(n)= $\sum_{d|n}\frac{n}{d}\phi(d)$ ;

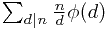现在证明,T(n)是一个积性函数

证明:

设 m , n 满足 (m,n)=1:

$T(n)=\sum_{d_n|n}\frac{n}{d_n}\phi(d_n)$

$T(m)=\sum_{d_m|m}\frac{m}{d_m}\phi(d_m)$

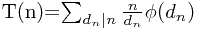
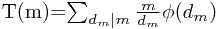
则:

$T(m)T(n)=(\sum_{d_m|m}\frac{m}{d_m}\phi(d_m))(\sum_{d_n|n}\frac{n}{d_n}\phi(d_n))$

$=\sum_{d_m|m}\sum_{d_n|n}\frac{mn}{d_md_n}\phi(d_m)\phi(d_n)$

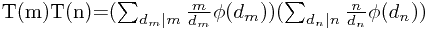
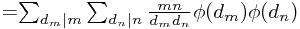
由于(m,n)=1,故dn与dm互素,所有dn,dm的组合正好取遍mn的约数

$T(m)T(n)=\sum_{d|mn}\frac{mn}{d}\phi(d)=T(mn)$

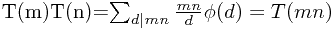
到了这里,只需考虑n等于素数的幂时T(n)的值:

根据T(n)的定义,显然有:

$T(p^k)=\begin{Bmatrix}2p-1 & k=1\\p\cdot T(p^{k-1})+\phi(p^k) & k>1\end{matrix}$

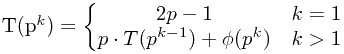
有了这个性质,就有可以在O(n)时间内用这个牛X的筛法把表打出来,然后求和还是O(n),查询什么的显然O(1)咯lol...

代码:

#include	<stdlib.h>
#include	<stdio.h>
#include	<string.h>
#include	<math.h>
#define FF(i,b) for(i=0;i<(b);i++)
#define FOR(i,a,b) for(i=(a);i<=(b);i++)
#define ZERO(x) do{memset(x,0,sizeof(x));}while(0)
#define SWAP(a,b) do{int _tmp=a;a=b;b=_tmp;}while(0)
#define INFI 2000000000
#define INFF 1e100
#define maxn 1000000
typedef long long  LL;
int p[maxn+1],ph[maxn+1],pk[maxn+1],T[maxn+1];
LL G[maxn+1];
void sevie()
{
	memset(p,0,sizeof(p));
	int i,j;
	p[0]=ph[0]=0;ph[1]=1;T[1]=1;
	for(i=2;i<=maxn;i++)
	{
		if(!p[i]){p[++p[0]]=i;ph[i]=i-1;pk[i]=i;T[i]=(i<<1)-1;}
		for(j=1;p[j]<=maxn/i;j++)
		{
			p[p[j]*i]=1;
			if(i%p[j]){
				ph[i*p[j]]=ph[i]*p[j];
				pk[i*p[j]]=p[j];
				T[i*p[j]]=T[i]*T[p[j]];
			}
			else{
				ph[i*p[j]]=ph[i]*p[j];
				pk[i*p[j]]=pk[i]*p[j];
				if(i==pk[i])T[i*p[j]]=p[j]*T[i]+ph[i*p[j]];
				else T[i*p[j]]=T[i/pk[i]]*T[pk[i]*p[j]];
				break;
			}
		}
	}
	G[0]=0;
	for(i=1;i<=maxn;i++)G[i]=G[i-1]+T[i]-i;
}
int main ( int argc, char *argv[] )
{
	sevie();
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		if(!n)break;
		printf("%lld\n",G[n]);
	}
	return EXIT_SUCCESS;
}

牛逼的线性时间筛法

这个牛B的筛法是在这里看到的

复杂度是线性的，扩展性超好～

自己YY了几个可以扩展的内容，权当模板～

#define N 1024
//niubee linear sevie method
int phi[N],//欧拉函数
    p[N],//素数表
    ld[N],//最小素因子
    ldt[N],//最小素因子的次数
    min_pk[N],//if p==ld[n],min_pk[n]=1+p+p^2+...+p^ldt[n];
    sig[N],//约数和
    nd[N];//因子数
//依赖性:min_pk<-sig;ldt<-nd;
void sevie()
{
	memset(p,0,sizeof(p));
	int i,j;

	phi[0]=0;phi[1]=1;//phi
	ld[0]=0;ld[1]=1;//ld
	ldt[0]=0;ldt[1]=1;//ldt
	min_pk[0]=0;min_pk[1]=1;//min_pk
	sig[0]=0;sig[1]=1;//sig
	nd[0]=0;nd[1]=1;//nd
	for(i=2;i<=N;i++)
	{
		if(!p[i]){
			p[++p[0]]=i;
			phi[i]=i-1;
			ld[i]=i;
			ldt[i]=1;
			min_pk[i]=i+1;
			sig[i]=i+1;
			nd[i]=2;
		}
		for(j=1;p[j]<=N/i;j++)
		{
			p[p[j]*i]=1;
			ld[p[j]*i]=p[j];
			if(i%p[j]){
				phi[p[j]*i]=phi[p[j]]*phi[i];
				ldt[p[j]*i]=1;
				min_pk[p[j]*i]=p[j]+1;
				sig[p[j]*i]=sig[i]*sig[p[j]];
				nd[p[j]*i]=nd[p[j]]*nd[i];
			}
			else{
				phi[p[j]*i]=phi[i]*p[j];
				ldt[p[j]*i]=ldt[i]+1;
				min_pk[p[j]*i]=p[j]*min_pk[i]+1;
				sig[p[j]*i]=sig[i]/min_pk[i]*min_pk[p[j]*i];
				nd[p[j]*i]=nd[i]/(ldt[i]+1)*(ldt[p[j]*i]+1);
				break;
			}
		}
	}
}